ИИ-модель «Машина Рамануджан» помогает математикам создавать новые гипотезы

^{Изображение: habr.com}

^{Математики Техниона, Израиль, разработали ИИ-модель, которая создает математические гипотезы. Ученые считают, что уже сегодня ИИ-модель может помочь в решении самых трудных проблем, которые стоят перед наукой сотни лет.}

^{Придумывать гипотезы приятно, а вот доказывать иногда очень трудно. Математики посматривали на ИИ с надеждой, что он освободит их от работы по доказательству гипотез. Но судя по всему, ему тоже больше нравится придумывать гипотезы, а доказательство он оставляет людям.}

^{Директор Лондонского института математики Томас Финк в своей колонке, которая была опубликована на сайте}^Nature^{, размышлял о влиянии ИИ на развитие математики. Финк приходит к выводу, что ИИ наиболее полезен не в том, на что многие надеялись: он еще долго не сможет оказывать математикам техническую помощь, то есть, строить корректные доказательства, но он почти быстро учится строить гипотезы и особенно плодотворно это делает в самой абстрактной области математики — теории чисел.}

^{Финг пишет: «Несколько лет назад компьютерная программа под названием „Машина Рамануджана“}^{предложила}^{новые формулы для фундаментальных констант, таких как π и e. Некоторые из этих гипотез ИИ с тех пор были доказаны, а другие остаются открытыми проблемами».}

Машина Рамануджан

^{«Машину Рамануджан» описали математики Техниона в 2021 году. Они на этом не остановились. Теперь вышла новая}^статья^{, которая во многом продолжает предыдущую работу.}

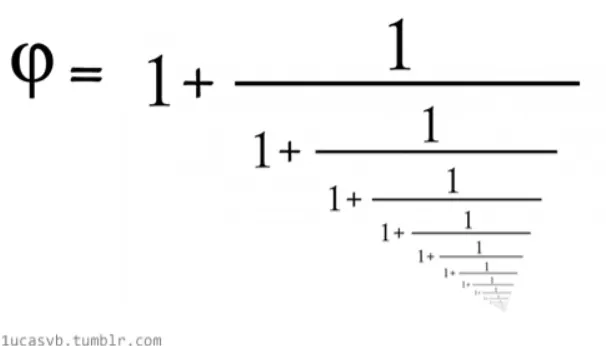
^{Главной идеей «Машина Рамануджан» было разложение чисел в цепные дроби. На рисунке приведено разложение в бесконечную цепную дробь константы «золотого сечения».}
^{Proceedings of the National Academy of Sciences (2024). DOI: 10.1073/pnas.2 321 440 121}

^{Математики}^{разработали}^{новую концепцию поиска гипотез, которая вдохновлена физикой. Ученые рассмотрели так называемые консервативные матричные поля. Они похожи на обычное электромагнитное или гравитационное поле, но «двигаются» в этих полях не частицы, а гипотезы. С этими гипотезами работает модель ИИ, которая отыскивает наилучшие предположения среди огромного множества допустимых.}

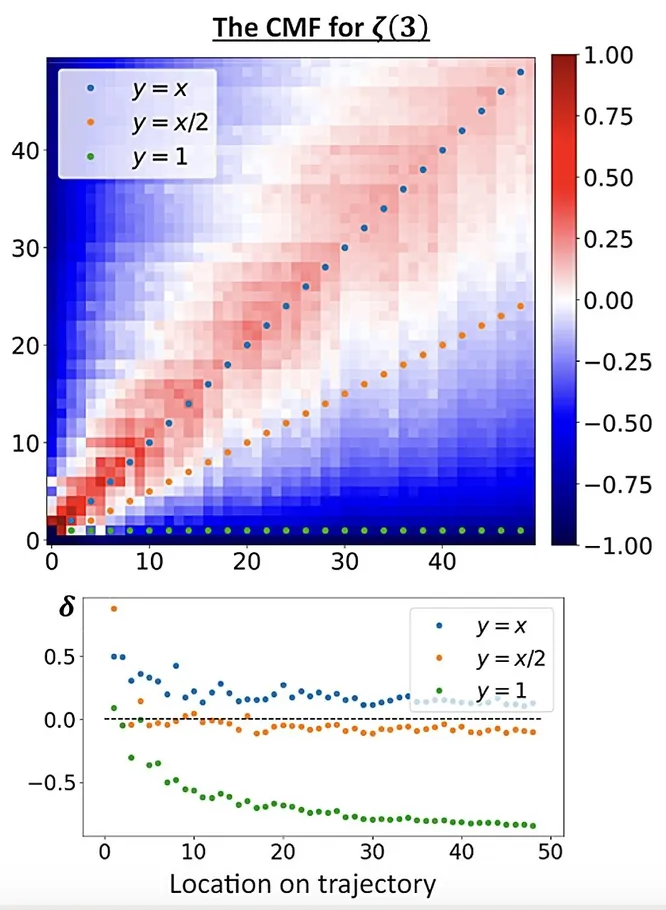
^{Доказательство иррациональности с помощью консервативного матричного поля. Существует множество способов доказать иррациональность константы, один из которых заключается в оценке величины, называемой «мерой иррациональности» (обозначается μ). Эта мера определяет, насколько хорошо рациональная последовательность может аппроксимировать число. Можно показать, что если все элементы последовательности отличны от предела и последовательность сходится к пределу достаточно быстро, то предел иррационален. Это «достаточно быстро» выражается величиной μ, и если она больше 0, то число иррационально. На графике показана мера иррациональности, полученная в каждой точке консервативного матричного поля константы Апери, обозначаемой ζ(3), отмечая различные пути в матричном поле. Красные пути обозначают последовательности с мерой иррациональности больше 0, что доказывает иррациональность константы ζ(3).}

^{Математики уже сейчас пытаются решить многие открытые проблемы, в том числе доказать иррациональность}^{чисел Каталана}^{. Эта гипотеза была сформулирована в середине XIX века и до сих пор не решена. Доказательство иррациональности}^{константы Апери}^{смотрите на рисунке. Другая важнейшая проблема, которой будет заниматься ИИ-модель, — это одна из самых знаменитых нерешенных задач математики — гипотеза Римана.}

^{Ученые Техниона выкладывают, полученные гипотезы на сайте «}^{Машина Рамануджан}^{» и предлагают всем желающим принять участие в их проверке и доказательстве.}